[10000印刷√] 扇形 弧の長さ 公式 891124-扇形 面積 弧の���さ 公式
扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
なぜ、θが微小なとき、tanθ≒θとなるのですか?直角三角形で考えてみましょう。tanθ は (底辺)分の(高さ) で表せますね。θ が 微小 と云う事は 高さが 微小(≒0) です。つまり 分数 そんな公式はありません。 円の面積、円周の長さ、又は 扇型の中心の角度の どれか 1つが分かっていないと、 扇型の弧の長さから 半径を求めることは出来ませんし、 半径から 扇型
扇形 面積 弧の長さ 公式
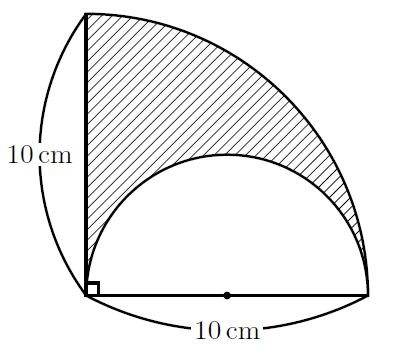
扇形 面積 弧の長さ 公式- 半径が3㎝、弧の長さが3 ㎝の扇形の中心角を求めなさい。 まずは、方程式を使って扇形を求める方法について解説していきます。 求めたい中心角を とおいて、方程式を作っていきおうぎ形の問題では弧の長さや面積を求める問題が出題されますが、それぞれ以下の公式で求めることができます。 おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 ×
扇形 扇形 計算サイト
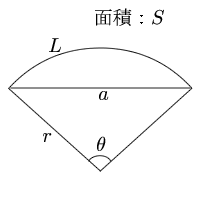
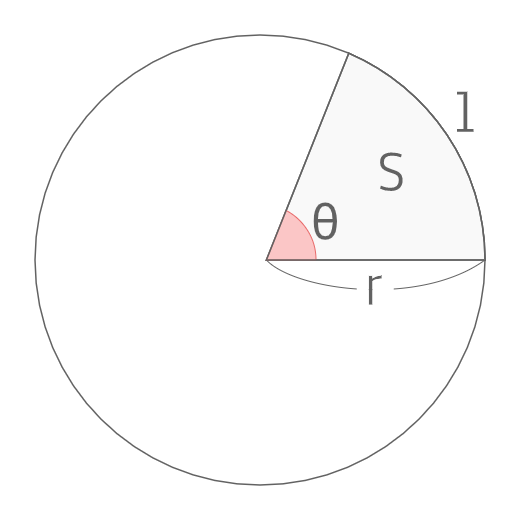
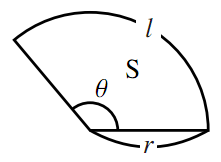
カテゴリマスター 22/9/8 713 扇形の 半径が、r 中心角が、θ (ラジアン) この長さが、l 面積が、S のとき、 l=r・θ S= (1/2)・r・l S= (1/2)・r²・θ (回答) 条件より、 弧の長 弧の長さが与えられているので、扇形の弧の長さを求める公式を使って考えていきましょう。 }{360}$$ まずは、求めたい半径の大きさを\(x\)㎝とします。 すると、半径\(x\)㎝で円錐の体積の求め方の公式って こんにちはこの記事をかいているKenだよ犬の散歩が趣味だね 円錐の体積の求め方の公式は 底面積高さ13 下の図は一般的な円です 円の面積はどのように求めればよ
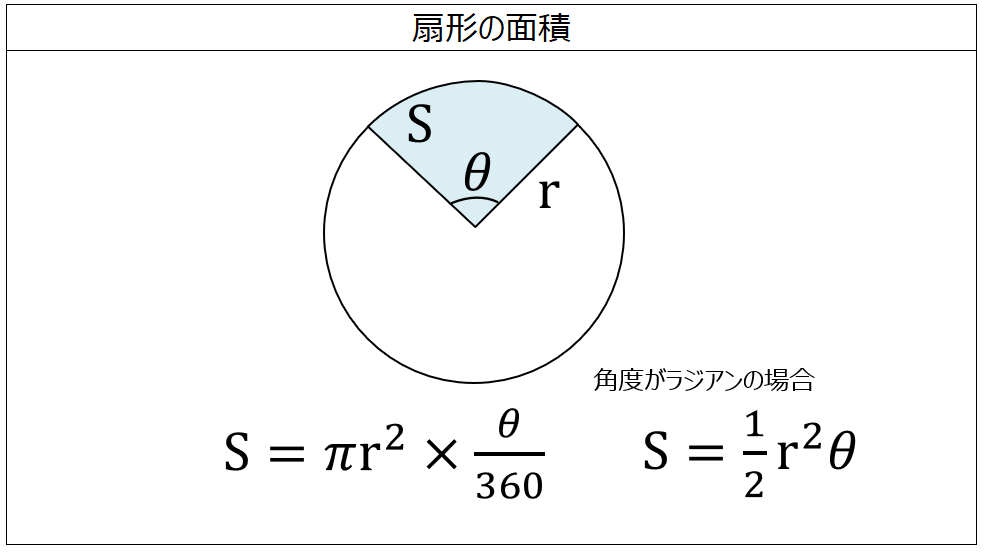
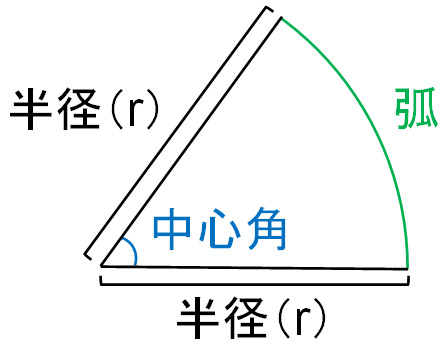
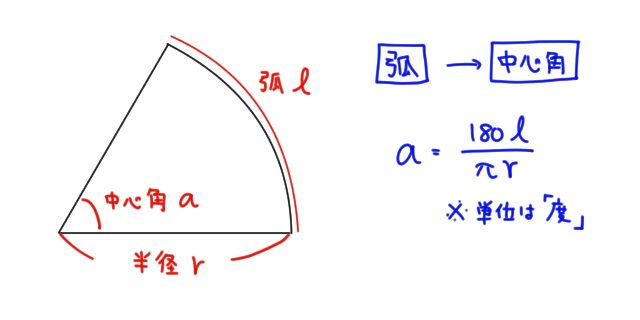
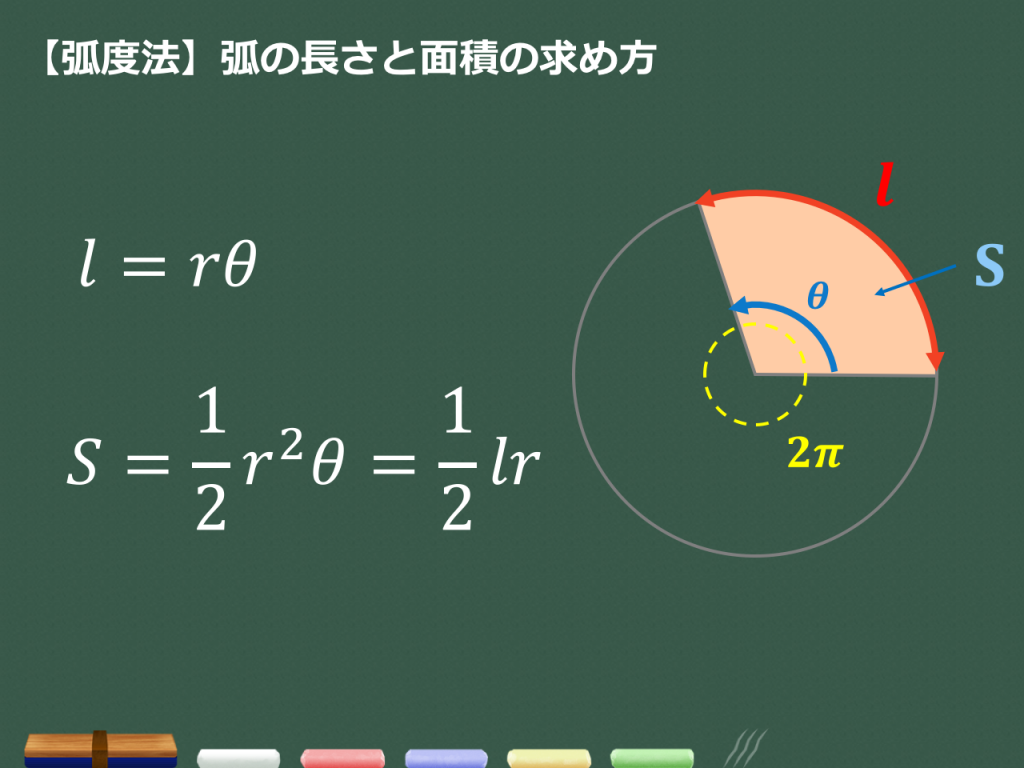
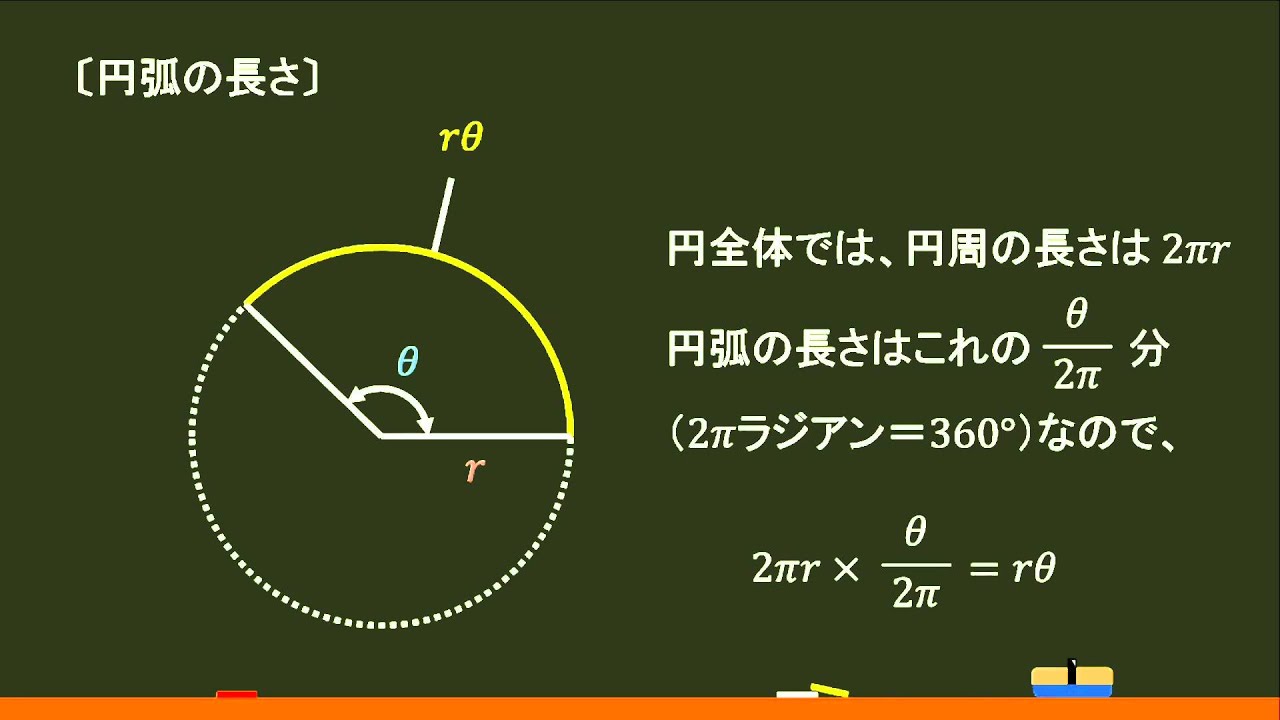
扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明 エンジニアの学習・コミュニティーサ 2分でわかる!扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね?? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円扇形の面積弧の長さ l l からの導出 1 2lr 1 2 l r 扇形の弧の長さ 2πr a 360 2 π r a 360 円周と直径との比は より大きく より小さい 注釈 3 を 取り尽くし法 を用いて証明した 出てくる文字の意味は
扇形 面積 弧の長さ 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 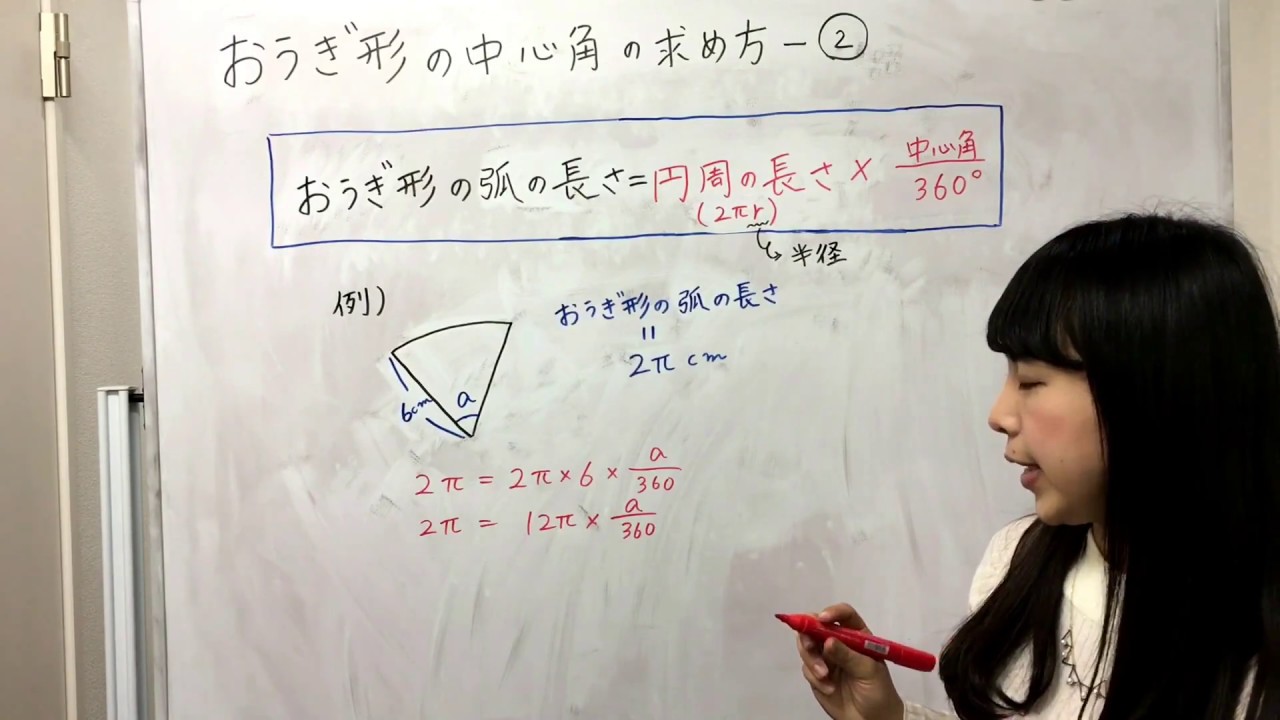 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 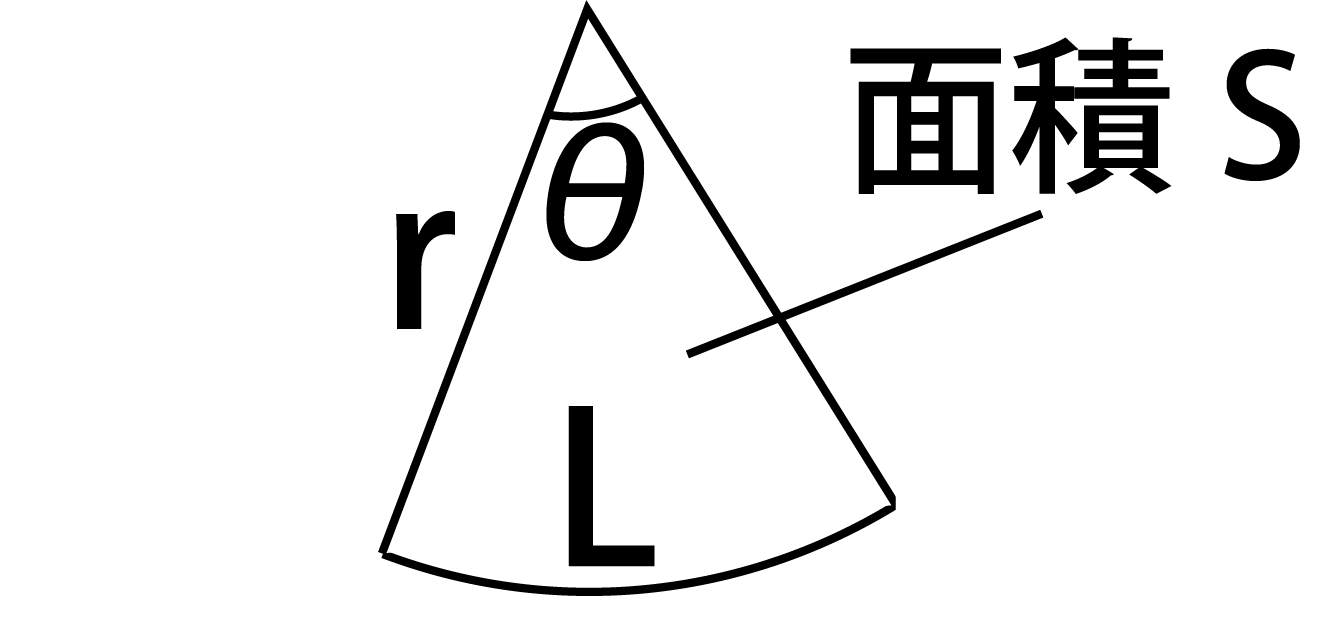 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 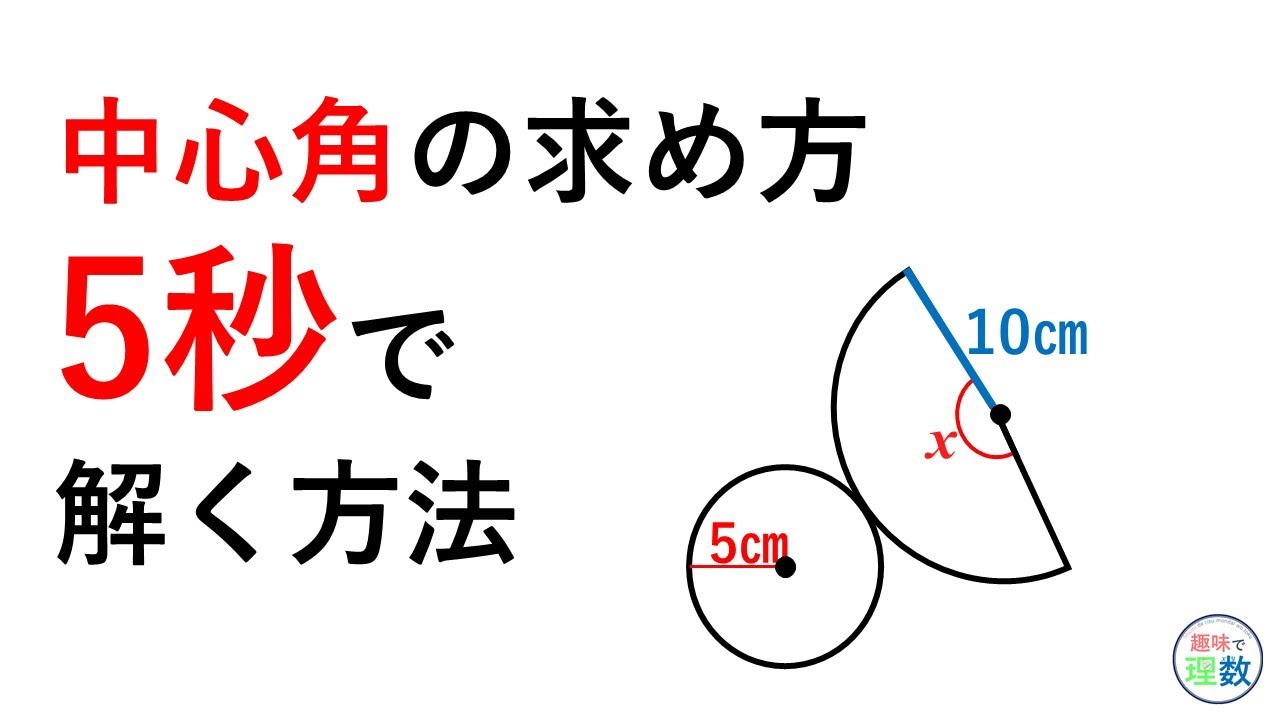 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 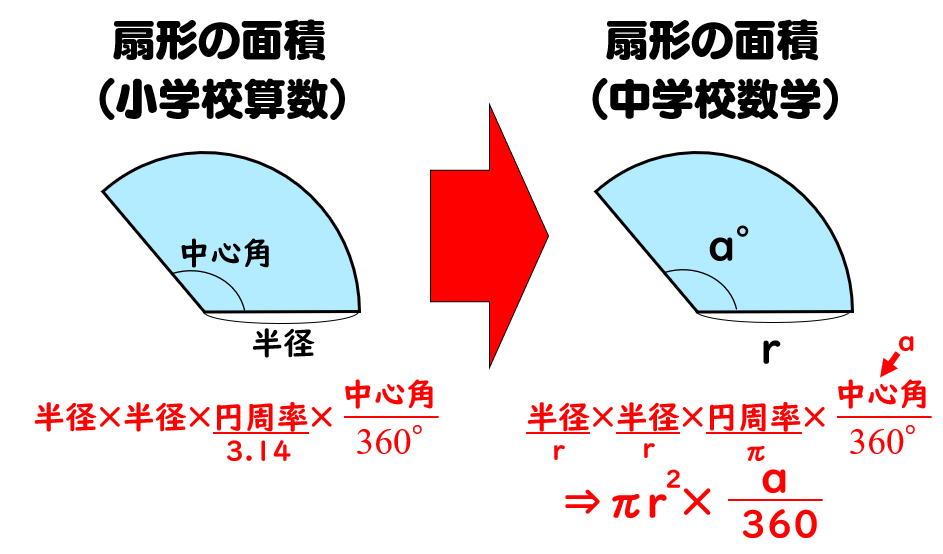 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 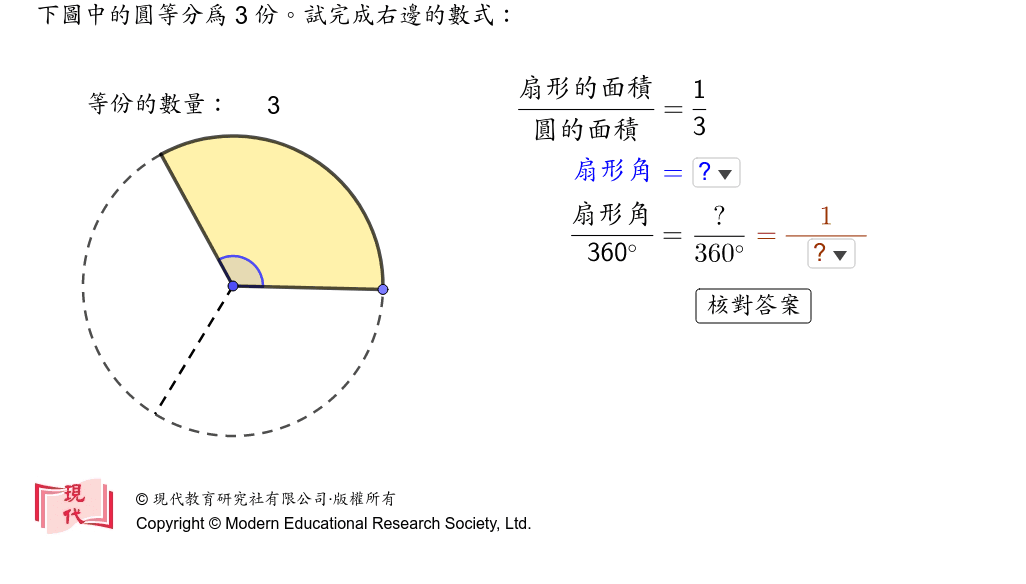 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 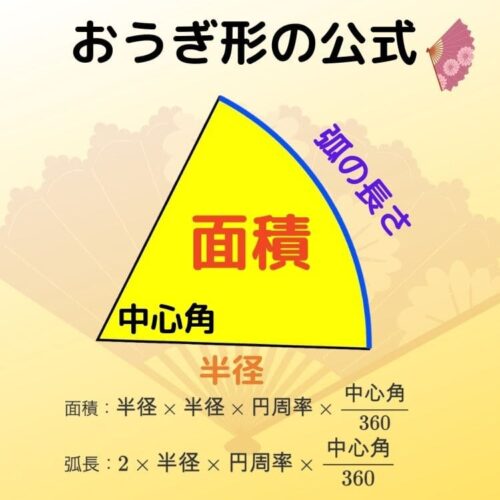 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 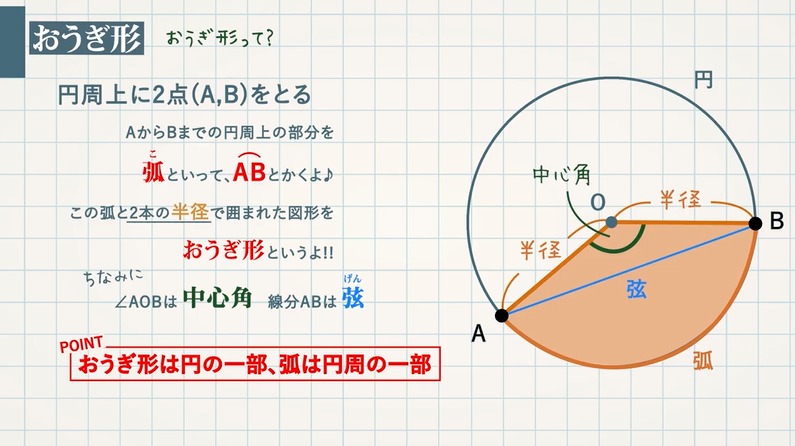 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 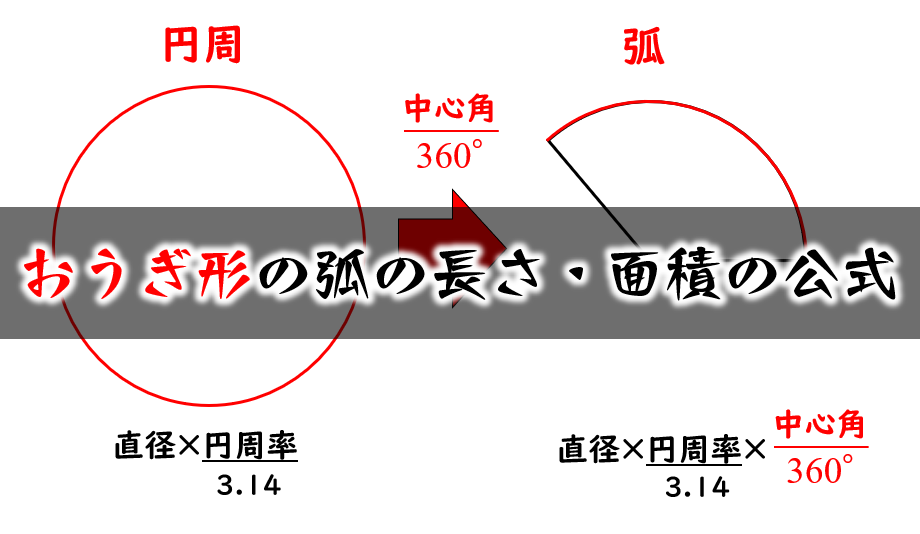 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 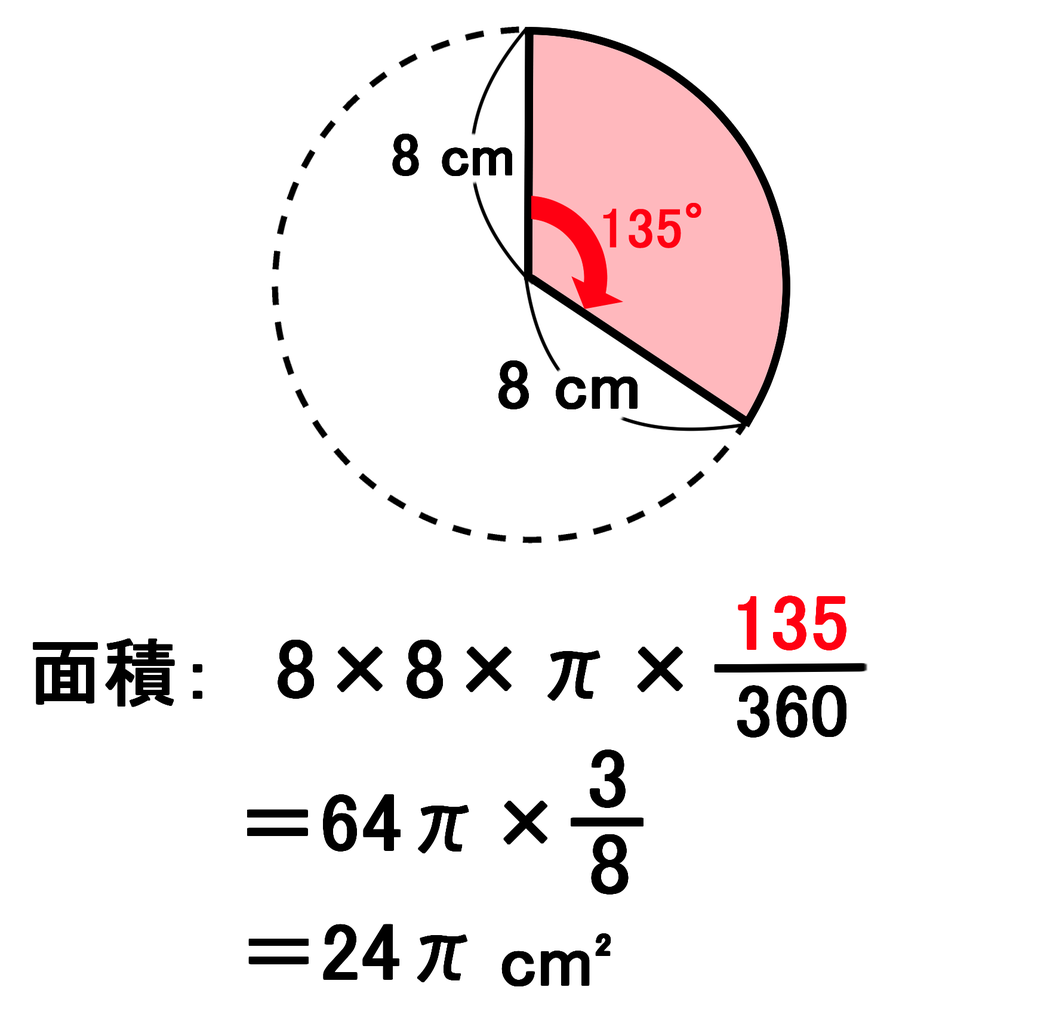 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 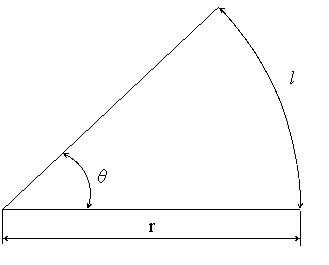 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 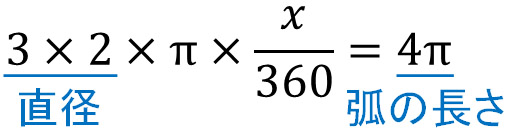 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 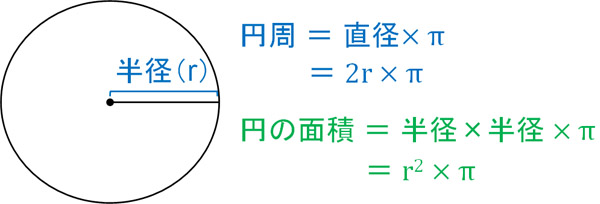 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | 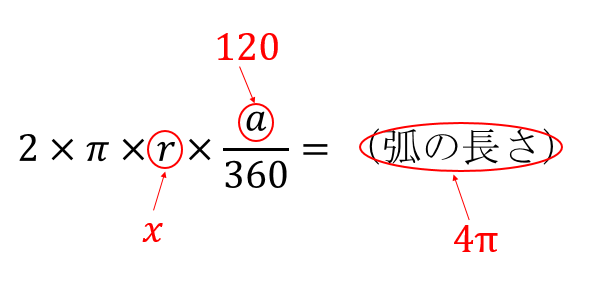 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |  おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ | おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ |
扇形の面積・弧の長さの計算機です。 角度を入力 面積は 0 π です 弧の長さは 0 π です π=とした時 面積は 0 です 弧の長さは 0 です ※円周率πは無理数ですので数扇形の弧の長さ L=rθ 扇形の面積 S=r^2θ/2=rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は?1分でわかる
Incoming Term: 扇形 弧の長さ 公式, 扇形 弧の長さ 公式 中学, 扇形 弧の長さ 公式 高校, 扇形 面積 弧の長さ 公式,
コメント
コメントを投稿